Notes
four squares vi solution
Solution to the Four Squares VI Puzzle
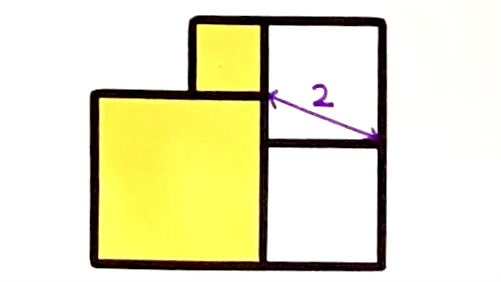
Four squares. What’s the total shaded area?
Solution by Pythagoras' Theorem
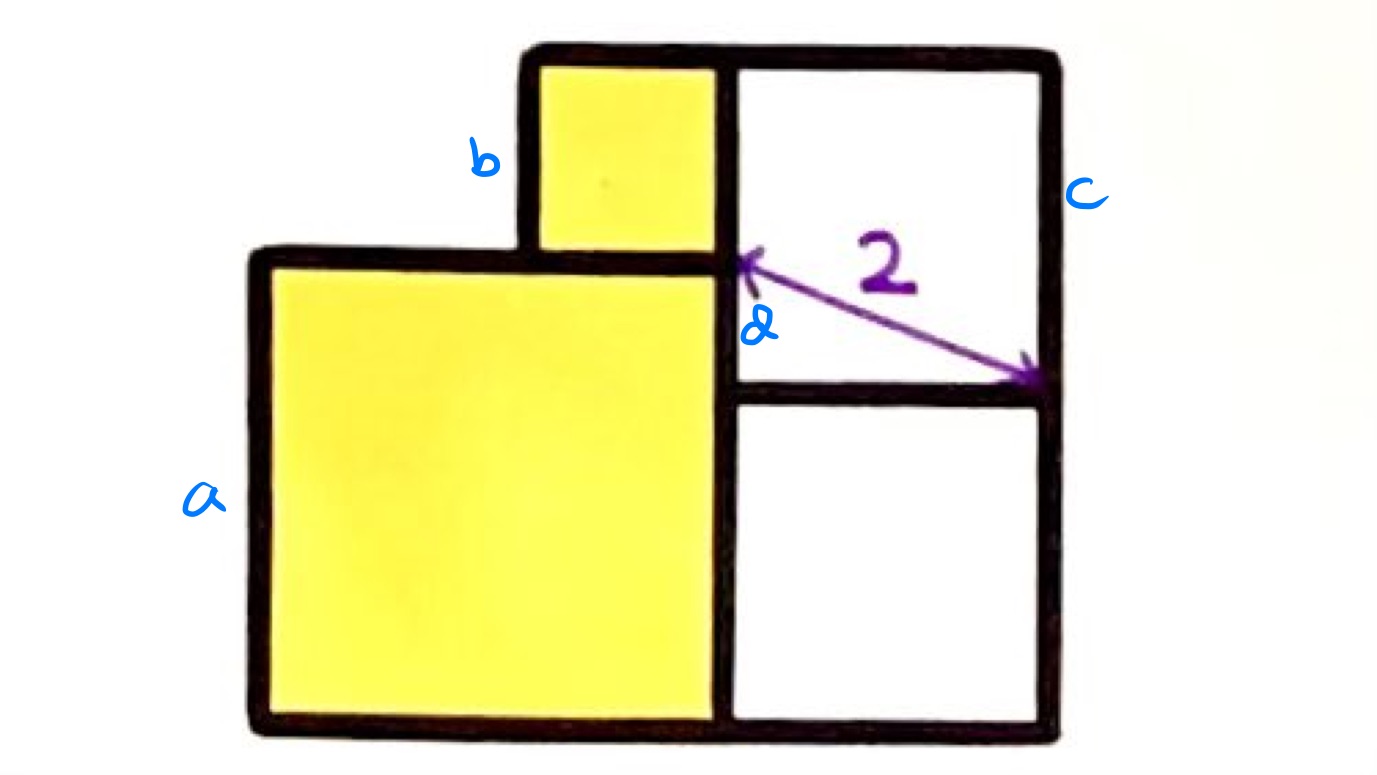
As in the above diagram, let , , and be the side lengths of the squares, and is the difference between the top of the large yellow square and the lower white square. Applying Pythagoras' Theorem to the triangle shows that:
From the diagram, and , so . Therefore:
Therefore